What is convolution
Convolution is the effect of multiplying
every sample in one wave or impulse by the samples
that are contained within another waveform. In a
sense, this feature uses one waveform to “model”
the sound of another waveform. The result can be that
of filtering, echoing, reverberating, phase shifting,
or any combination of these effects.
For
example, “convolving” someone saying “Hey”
with a drum track (short full spectrum sounds such as
snares work best) will result in the drums saying
“Hey” each time they are hit.
With the proper impulses, any reverberant space can
be simulated. For example, if you have an impulse of
your favorite cathedral, and convolve it with any
audio, then the result would sound as if that audio
were played in that cathedral.
You can generate an impulse like this by going to the
cathedral in question, standing in the spot where you
would like the audio to appear it is coming from, and
generating a loud impulsive noise, like a “snap”
or loud “click”. You can make a stereo
recording of this “click” from any location
within the cathedral. If you used this recording as
an impulse, then convolution with it will sound as if
the listener were in the exact position of the
recording equipment, and the audio being convolved
were at the location of the “click”.
What
is an impulse response file
An “impulse response file” is the
data by which every other sample in your waveform
will be multiplied. If the impulse is a single sample
of a full volume “tick”, then the
convolution of that impulse with any audio data will
just be that audio data itself. If that “tick”
is at half volume, then the original audio data will
be reproduced at half volume.
If
there are several ticks, descending in amplitude over
time, such as one tick every 100 milliseconds, and
half as loud as the previous tick (fig. 2), then the
result of convolution (fig. 3) with some audio (fig.
1) will be that sound echoed with 100ms between each
echo, and each echo at half the volume of the
previous echo.
Another
interesting use for convolution is to generate an
infinite sustained sound of anything. For example,
one singing “aaaaaah” for one second could
be turned into thousands of people singing “aaaaaah”
for any length of time by using some white noise.
| Example 1 |
Source : snare drum
ex1_src1.wav
36 KB
(mono-44KHz-16bit) |
Impulse : 100 ms spaced decaying
tics
ex1_imp1.wav
69 KB
(mono-44KHz-16bit) |
Convolution result :
ex1_res1.wav
82 KB
(mono-44KHz-16bit) |
| Example 2 |
Source : man voice
ex2_src2.wav
454 KB
(mono-44KHz-16bit) |
Impulse : Metallic delay effect
ex2_imp2.wav
517 KB
(stereo-44KHz-16bit) |
Convolution result :
ex2_res2.wav
1'165 KB
(stereo-44KHz-16bit) |
| Example 3 |
Source
: snare drum
ex1_src1.wav
36 KB
(mono-44KHz-16bit) |
Impulse
: 4 s decaying white noise
ex3_imp3.wav
690 KB
(stereo-44KHz-16bit) |
Convolution
result :
ex3_res3.wav
760 KB
(stereo-44KHz-16bit) |
To
get a feel of convolution, load up and play with some
of the sample Impulse files on this page using your
favorite hardware or software convolver.
Enjoy !
A
bit more about convolution
Imagine the following example :
An audio file containing 8 samples (X0 to X7) convolved
with an impulse file containing 4 samples (i0 to i3).
That would give the following table :
| Source file samples (Xn) |
X0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
|
|
| Impulse file samples (ik) |
i0
|
i1
|
i2
|
i3
|
|
|
|
|
|
|
|
| |
i0 X0
|
i0 X1
|
i0 X2
|
i0 X3
|
i0 X4
|
i0 X5
|
i0 X6
|
i0 X7
|
|
|
|
| |
|
i1 X0
|
i1 X1
|
i1 X2
|
i1 X3
|
i1 X4
|
i1 X5
|
i1 X6
|
i1 X7
|
|
|
| |
|
|
i2 X0
|
i2 X1
|
i2 X2
|
i2 X3
|
i2 X4
|
i2 X5
|
i2 X6
|
i2 X7
|
|
| |
|
|
|
i3 X0
|
i3 X1
|
i3 X2
|
i3 X3
|
i3 X4
|
i3 X5
|
i3 X6
|
i3 X7
|
This
can be represented by the following diagram :
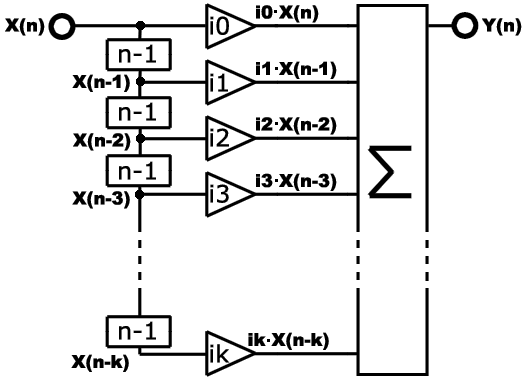
Which
correspond to the following expression :
Y(n) = i0 · X(n) + i1 · X(n-1)
+ i2 · X(n-2) + i3 · X(n-3) + ... + ik · X(n-k)
Or
to the following general equation :
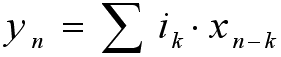
|

